はじめに：ディープラーニングの概要
皆さん、ディープラーニング（深層学習）という言葉はもう聞いたことがありますよね？これは人工知能（AI）の一分野で、多層のニューラルネットワークを用いてコンピュータが自らデータから特徴を学習する技術です。従来の機械学習では、どの特徴に注目すべきか人間が設計していましたが、ディープラーニングでは層が深く重なったニューラルネットワークがデータから重要な特徴を自動抽出し、複雑なパターンも捉えられる点が画期的です。2010年代以降、計算資源（GPU）の発達とビッグデータの蓄積によりディープラーニングが飛躍的に性能向上し、画像認識や自然言語処理、ゲームAI（AlphaGoなど）で人間を凌ぐ成果が報告され注目を集めました。
本記事では、JDLA「G検定（ジェネラリスト検定）」の受験対策にも役立つように、ディープラーニングの基本概念を解説します。ニューラルネットワークとディープラーニングの違いから始め、活性化関数、誤差関数（損失関数）、正則化、誤差逆伝播法、そして最適化手法まで、短時間で要点を掴めるよう構成しました。それぞれのセクションではG検定で押さえるべきポイントも太字でまとめていますので、学習の確認に役立ててください。それでは、ディープラーニングの世界を一緒に見ていきましょう！
ニューラルネットワークとディープラーニングの違い
最初に、「ニューラルネットワーク」と「ディープラーニング」の違いについて整理しましょう。ニューラルネットワークとは、人間の脳の神経細胞（ニューロン）の結合をヒントに作られたアルゴリズムで、入力層・中間の隠れ層・出力層から構成されます。従来は隠れ層が1～2層程度の浅い（shallow）構造が一般的で、比較的シンプルなパターン認識に用いられてきました。一方でディープラーニング（深層学習）では、隠れ層を何十層も重ねた深い（deep）ニューラルネットワークを使うことが特徴です。層を深くすることで表現できる複雑さが増し、より高度で抽象的な特徴を自動的に学習して人間が気づきにくいパターンまで捉えることが可能になります。
具体例として、画像認識では昔はエッジや色などの特徴を人手で設計してニューラルネットに入力していました。しかしディープラーニングでは、生のピクセルデータを多層ネットワークに与えるだけで、初層でエッジを捉え、中間層でパーツを捉え、最終層で物体全体を認識する、といった階層的な特徴抽出が実現できます。これは、人間が「あらかじめ特徴を決めて教える」アプローチとは大きく異なる点です。
また、ディープラーニングの躍進を支えたのが大規模データと高性能GPUです。浅いニューラルネットでもある程度の学習は可能ですが、深層ネットワークはより多くのパラメータ（重み）を持つため大量のデータで学習することで真価を発揮します。例えば画像認識コンテストにおいて、多層CNN（畳み込みニューラルネット）が従来手法を圧倒した2012年の出来事（AlexNetの成功）は有名です。このようにディープラーニングは「層を深くしたニューラルネットワークによる機械学習」と捉えることができます。
G検定で押さえるべきポイント:
- ディープラーニング = 多層（深層）ニューラルネットワークによる学習。 従来のニューラルネットが隠れ層1～2層の浅い構造だったのに対し、ディープラーニングでは多数の層を重ねることで高度な特徴を自動学習できる。
- 特徴抽出の違い: 浅いニューラルネットワークや従来の機械学習では人が特徴量を設計していたが、ディープラーニングでは多層ネットワークが生データから特徴を自動抽出する。この違いが深層学習の大きな強みとなっている。
活性化関数（Activation Function）
次に、ニューラルネットワークの各ニューロンで使われる活性化関数について学びましょう。活性化関数とは、ニューロンへの総入力に対し出力を計算する関数で、ネットワークに非線形性を与える重要な役割があります。例えばあるニューロンの計算は「総入力の線形和」をまず求め、それに活性化関数
を適用して出力を得ます。ここでが単なる恒等関数（入力をそのまま出力）だと、ネットワーク全体は入力に対して線形変換を繰り返しているだけになってしまいます。線形変換を何層重ねても結果は線形のままであり、これではどんなに層を増やしても1層のモデルと本質的に変わりません。したがって、ニューラルネットには非線形な活性化関数が不可欠です。活性化関数によってネットワークは複雑な非線形のパターンを学習できるようになります。
では代表的な活性化関数を見てみましょう。歴史的にはシグモイド関数（S字カーブを描く関数）がよく使われてきました。しかし現在では深い層を持つネットワークではシグモイドはほとんど使われません。その理由の一つは、シグモイドでは入力が大きく正負に振れると勾配（傾き）が限りなく0に近づいてしまう「勾配消失問題」が起きやすく、学習が進まなくなるためです。そこで近年主流となっているのがReLU (Rectified Linear Unit)と呼ばれる活性化関数です。ReLUは0以下の入力では出力0、正の入力ではそのまま出力とする非常にシンプルな関数ですが、入力が大きくなっても勾配が一定で勾配消失を起こしにくいという利点があります。これにより深い層の学習が安定しやすく、現在多くのモデルで採用されています。
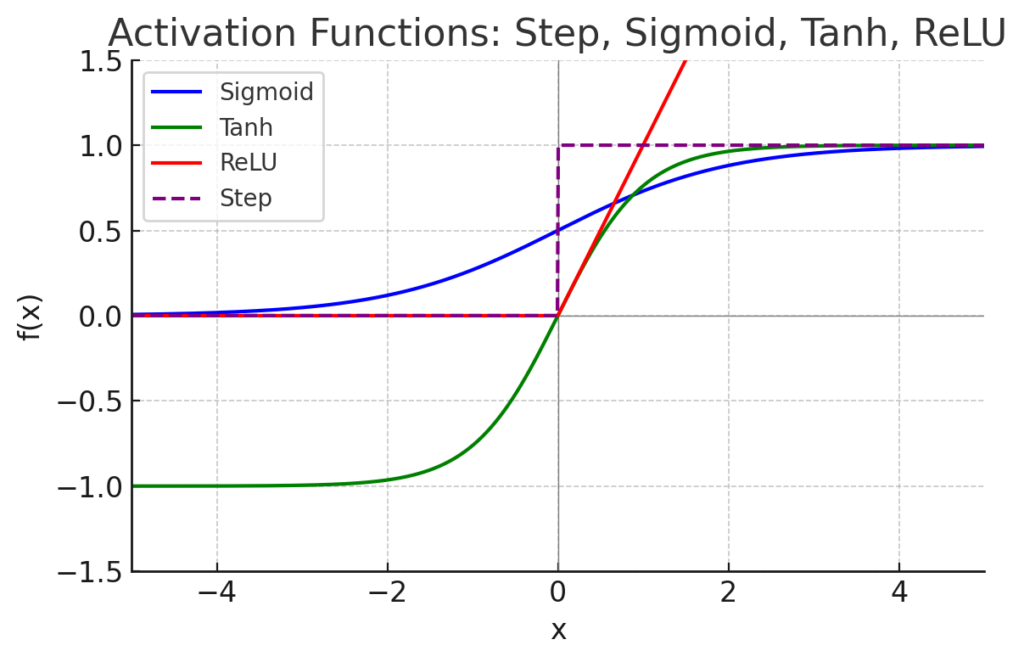
図1: 主要な活性化関数4種の出力の比較（横軸は入力値
）。Step関数（紫破線）は0を境に出力が0/1に切り替わる閾値関数、Sigmoid関数（青線）はS字状に0～1の間で連続出力するが入力の絶対値が大きい領域で勾配が小さくなる傾向がある。tanh関数（緑線）は
～
の間で出力しシグモイドよりゼロ中心だが挙動は類似する。ReLU関数（赤線）は入力が負の場合0、正の場合は入力に比例して線形に増加する。ReLUは負側で勾配0だが正側は勾配一定であり、大きな入力でも勾配が消えない点が深層学習で好まれる理由である。
代表的な活性化関数を以下に箇条書きでまとめます：
- ステップ関数（閾値関数）: 一定の閾値を境に0か1を出力する関数。パーセプトロン(単純な二値分類モデル)で用いられるが、不連続で微分不可能なため現在のディープラーニングでは使われません。
- シグモイド関数（ロジスティック関数）: なめらかなS字曲線で0～1の実数を出力に返す関数。ニューラルネット黎明期にはよく使われましたが、入力の絶対値が大きくなると勾配がほぼ0になり学習が停滞する勾配消失が問題になります。
- tanh関数（双曲線正接関数）: 出力が～になるシグモイドの変種で、グラフはシグモイドを上下に広げてゼロ中心にした形です。シグモイド同様に大きな入力で勾配が小さくなる性質がありますが、出力の平均が0に近いためシグモイドよりは使いやすく、一部のネットワークで利用されます。
- ReLU関数（正則化線形関数）: 現在最も一般的な活性化関数。入力が正のときはそのまま出力し、負のときは0を出力します。計算が高速で勾配も広い範囲で一定なため深い層の学習に適しています。ただし負の値に対して常に勾配0となるため、学習中にニューロンがまったく活性化しなくなる「Dead ReLU」問題もあります。その対策としてLeaky ReLUやELUといった変種も提案されています。
G検定で押さえるべきポイント:
- 活性化関数はネットワークに非線形性を与える鍵。 活性化関数が非線形でないと、多層ニューラルネットワークでも線形変換の繰り返しにすぎず、1層のモデルと変わらなくなってしまうしたがって「なぜ非線形関数を使うのか」を理解しておくこと。
- 主要な活性化関数の特徴: シグモイドやtanhは出力が飽和すると勾配消失しやすいため、層の深いネットではほとんど使われなくなった。ReLUは現在のデファクトスタンダードで、勾配消失の問題を緩和し深層でも学習を安定させる働きがある。G検定では各関数の長所・短所（例えば「ReLUはなぜ優れているか」等）も問われる可能性がある。
誤差関数（損失関数）
続いて、誤差関数（ごさかんすう）について説明します。誤差関数は損失関数とも呼ばれ、モデルの予測結果と正解（教師データ）とのズレを数値で表す関数です。簡単に言えば、「どれだけ予測が間違っているか」を計算するためのものですね。この誤差（損失）の値が小さいほどモデルの予測性能が高い（誤差が少ない）ことを意味します。ディープラーニングにおける学習では、誤差関数の値を最小化するようにモデルのパラメータ（重みやバイアス）を調整していきます。最終的に誤差関数の値が十分小さくなれば、モデルが訓練データ上で高い精度を発揮していることになります。
誤差関数には様々な種類がありますが、タスク（分類か回帰か）に応じて適切なものを選ぶのが一般的です。分類問題（例：画像がネコか犬かを当てる）では、モデルが各クラスである確率を出力し、それと正解ラベルとの誤差を測る交差エントロピー損失がよく使われます。交差エントロピーは2つの確率分布の差異を測る指標で、モデルが正解クラスに高い確率を割り当てるほど損失が小さくなる仕組みです。一方、回帰問題（例：家賃の予測など連続値を当てる）では、平均二乗誤差 (MSE)が代表的です。これは「予測値と正解値の差」を2乗して平均した値で、差（誤差）が大きいほど値も大きくなり、これを最小化することで予測精度が向上します。MSEは外れ値に弱い欠点がありますが、シンプルで扱いやすいため広く使われています。外れ値に頑健な平均絶対誤差 (MAE)や、MSEとMAEの折衷であるHuber損失なども回帰で用いられます。
ポイントとして、分類か回帰かで誤差関数を使い分けることを覚えておきましょう。例えばクラス分類では交差エントロピー、それ以外にSVMなどでヒンジ損失を使う場合もあります。回帰ではMSEやMAEが基本です。また、モデルの種類によっては独自の損失関数（例：GANの識別器と生成器の損失など）を設計することもあります。いずれにせよ、「誤差関数の値を小さくする」=「モデルを良くする」という構図を押さえておきましょう。
G検定で押さえるべきポイント:
- 誤差関数とは何か？ モデルの予測と正解のズレ（誤差）を定量化した関数であり、学習ではこの値を最小化するように重みを更新していく。「損失関数」「コスト関数」と呼ばれることも同義なので、用語の言い換えにも注意。
- 代表的な誤差関数と適用先: タスクに応じた損失関数の使い分けを理解すること。分類問題では交差エントロピー損失が一般的（確率出力の誤差を測る）。回帰問題では平均二乗誤差 (MSE)が基本（予測値と実測値のズレを二乗平均）。外れ値が多い場合はMAEやHuber損失、二値分類でSVMならヒンジ損失など、ケースに応じた典型も合わせて押さえる。
正則化（Overfitting対策）
モデルの学習が進むと、訓練データに対する誤差はどんどん小さくなります。しかし注意しなければならないのは、行き過ぎた最適化は「過学習（オーバーフィッティング）」を引き起こすことです。過学習とは、モデルが訓練データにあまりに適合しすぎるあまり、新しいデータへの汎化性能（一般化能力）が低下してしまう現象です。例えば訓練データ上の誤差を極端にゼロ近くまで下げたモデルが、テストデータでは全然当たらない…というのは過学習が疑われます。ディープラーニングの強力な表現力ゆえに、この過学習は放っておくと起こりやすい問題です。
そこで重要になるのが正則化（Regularization）という考え方です。正則化とは、モデルが複雑になりすぎないようペナルティを与えることで過学習を防ぐ手法の総称です。簡単に言うと「モデルの自由度にブレーキをかけてあげる」テクニックですね。これにより訓練データに対する完璧な当てはまり（フィッティング）を少し犠牲にしてでも、未知のデータに対する汎化能力を高めることができます。
代表的な正則化手法として、
正則化と
正則化があります（それぞれラッソ、リッジ回帰として統計モデルにも対応します）。これらは誤差関数にモデルパラメータの大きさに応じたペナルティ項を加える方法です。具体的には、
- 正則化: モデルの全ての重みの絶対値の総和をペナルティとして誤差関数に加える手法。これによって重要でない重みは0に近づき、最終的に一部の重みがゼロになる（特徴選択が行われる）効果があります。高次元データで不要な入力特徴を削減したい場合に有効です。
- 正則化: 全ての重みの二乗の総和をペナルティとして加える手法。重み全体の大きさを均しく小さくしようと働き、異常に大きな重みを抑制します。ではのように重みが完全に0にはなりにくいですが、モデルをなだらかに（平滑に）する効果があります。
ディープラーニングで非常によく使われる正則化手法にドロップアウト (Dropout)があります。ドロップアウトは、学習時にニューラルネットワークの隠れ層のニューロンをランダムに一定割合無効化（出力を0に）するという手法です。例えば隠れ層の50%のニューロンを無作為に消して学習させる、といった具合です。一見奇妙に思えるかもしれませんが、毎回異なるサブネットワークで学習を行うことになり、結果的に多数のモデルをアンサンブルしているような効果が得られます。これによって特定のニューロン（特徴）に過度に依存することを防ぎ、過学習を抑制します。ドロップアウトはシンプルながら非常に有効で、多くのモデルで標準的に使われています。
他にも早期終了（Early Stopping）も実践的な正則化手法です。これは、訓練データに対する誤差は下がっているのに検証データに対する誤差が下がり止まって上がり始めたタイミングで、訓練（重みの更新）を打ち切る方法です。要は「これ以上学習すると過学習に入るサイン」が見えたらストップするというわけです。早期終了は追加の計算コストもなく手軽に過学習を防げるため、ディープラーニングでもしばしば用いられます。
G検定で押さえるべきポイント:
- 正則化の目的: 過学習（オーバーフィット）を防ぐこと。 モデルの複雑さにペナルティを課すことで、訓練データへの適合を少し犠牲にしてでも汎化性能を高める。G検定では「正則化とは何か？」に答えられるよう、平易な言葉で説明できると良いでしょう。
- 正則化 vs 正則化: は重みの絶対値和ペナルティで疎なモデル（不要な重みが0）を得る。は重みの二乗和ペナルティで滑らかなモデル（全ての重みを小さく）を得る。それぞれの効果の違い（特徴選択効果や異常値抑制）を押さえる。
- ドロップアウト: ニューラルネットのニューロンをランダムに無効化して学習する手法。多数のモデルをアンサンブルしているのと同等の効果があり、過学習を大きく低減できる。実装も簡単なため深層学習で広く使われる。
- その他の過学習対策: 早期終了やデータ拡張（データ増強）、バッチ正規化（内部表現の分布を安定化させ結果的に過学習を抑制する副次効果あり）なども覚えておくと望ましい。
誤差逆伝播法（バックプロパゲーション）
ここまで、入力から出力を得て誤差（損失）を計算する流れを学びました。では、その誤差をどのようにして各重みにフィードバックし、重みを更新しているのでしょうか？ その核心を担うアルゴリズムが誤差逆伝播法（バックプロパゲーション）です。誤差逆伝播法は1980年代に考案された手法で、現在のディープラーニングの重み学習の事実上の標準となっています。
簡単に言うと、誤差逆伝播法は出力側で計算された誤差（損失関数の勾配）をネットワークの入力側へ逆方向に伝えていくことで、各層・各重みがどれだけ誤差に寄与したか効率的に計算するアルゴリズムです。具体的には、出力層では予測と正解の差から損失
の勾配
をまず計算し、そこからチェインルール（連鎖律）を用いて1つ前の層の勾配
、さらにその前の層…と逐次的に誤差を遡っていきます。こうして最終的に各重み
についての損失勾配
が求まるので、その勾配の符号と大きさに応じて重みを更新します（一般には勾配降下法で
と更新）。
誤差逆伝播法の優れている点は、この勾配計算をネットワークの構造に沿って体系的かつ高速に行えることです。層ごとに勾配計算を局所的に行い、それを伝搬して再利用していくため、もし素朴に全重みに対して偏微分を計算するよりもはるかに効率的です。特にディープラーニングでは層数・パラメータ数が非常に多いので、誤差逆伝播法なしでは現実的な時間で学習を行うことは困難でしょう。現在の主要な深層学習フレームワーク（TensorFlowやPyTorchなど）も、このバックプロパゲーションを自動微分機能として実装し、ユーザが意識せずとも勾配計算・重み更新が行われるようになっています。
バックプロパゲーション自体は数学的にはチェインルールの応用に過ぎませんが、1986年にRumelhartらがその有用性を示して以来、ディープラーニング復興の原動力となりました。G検定では「誤差逆伝播法とは何か？」や、「なぜ必要か？」を説明できることが求められます。難しい数式よりも、「多層パーセプトロンの重み学習を可能にした画期的手法」くらいの位置づけで理解しておくと良いでしょう。
G検定で押さえるべきポイント:
- 誤差逆伝播法の役割: ネットワークの出力誤差を入力方向へ伝搬させながら、各重みの勾配を効率よく計算するアルゴリズム。これにより多層ネットワークでも素早く最適な重み調整が可能になった。
- ディープラーニングに不可欠: 層が増えパラメータが非常に多くなるディープラーニングでは、誤差逆伝播法なしに勾配計算を行うのは非現実的。バックプロパゲーションは深層学習の学習を支える基盤技術である。
- チェインルールの応用: G検定では詳細な導出よりも概念理解が重視されるが、一応「連鎖律を用いて層ごとに勾配を遡っていく」ことは知っておく（例えば「出力層から順に微分を伝えていく」といった言い回しで説明可能）。また、近年話題になった勾配消失問題（特にシグモイド多用のRNNで顕在化）も、逆伝播の勾配が途中で極端に小さくなる現象なので関連知識として押さえる。
最適化手法（Optimizer）
最後に、最適化手法（オプティマイザー）について説明します。最適化手法とは、一言でいうとモデルの重みをどのように更新するか決めるアルゴリズムのことです。ディープラーニングの学習では、誤差逆伝播法で求めた勾配情報を使って重みを更新し、損失関数の値をできるだけ小さくすることが目的でしたね。最適化手法はまさに、この「損失を効率よく減らすにはどう重みを変化させるか」を定めるルールと言えます。最適化アルゴリズム次第で学習の速さや安定性が大きく変わるため、深層学習において非常に重要なトピックです。
基本となるのは最急降下法（勾配降下法, Gradient Descent）です。これは現在の重みについての損失関数の勾配
を計算し、そのマイナス方向（損失が減る方向）に重みを少しずつ更新する方法です。シンプルに言えば「坂道を転がり落ちるボール」のイメージで、損失の谷底に向かって重みを調整していくわけです。実際のディープラーニングでは、全データに対して勾配を計算するのではなく、データの一部（ミニバッチ）から近似的な勾配を得て更新するのが一般的です。ここでいくつか手法の違いを整理すると:
- バッチ勾配降下法 (Batch Gradient Descent): 訓練データ全体の誤差の勾配を計算し、一回の重み更新で全データ分まとめて更新する方法。理論的には安定しますが、大規模データでは1回の更新に時間がかかります。また、局所的な最適解に陥ると抜け出しにくいという欠点もあります。
- 確率的勾配降下法 (SGD): 毎回ランダムに1つのデータだけを使って勾配を計算し、重みを更新する方法。更新ごとにデータ一点の情報しか見ないため勾配にノイズがありますが、そのランダム性ゆえに局所解から抜け出しやすい利点があります。大規模データでも逐次1件ずつ処理するので効率的です。
- ミニバッチ勾配降下法: 少数（例:16や32件）のデータをひとまとめにして勾配計算・更新を行う手法。バッチGDとSGDの中間で、計算の並列化効率と勾配の安定性のバランスが取れており、現在のディープラーニングではこのミニバッチ方式が主流です。
上記の基本形に加えて、より高速に収束させたり安定化させるために勾配の更新方法に工夫を加えた手法が多数考案されています。代表的なものを挙げると:
- モーメンタムSGD (Momentum): 運動量の概念を取り入れ、勾配の移動平均（慣性）で重み更新を行う手法です。イメージとしては、ボールが谷を転がるときに勢いがつくように、勾配方向の変化をなだらかにします。これにより、谷底付近で勾配がジグザグしてなかなか進まないようなケース（振動）を抑制し、より速く収束する効果があります。
- AdaGrad: 各パラメータごとに適応的に学習率を調整する手法です。頻繁に大きな勾配が出るパラメータは学習率を下げ、あまり変化しないパラメータは高めの学習率を保つことで、それぞれ適切な速さで最適化を進めます。特に疎な（ほとんどゼロの）特徴を持つデータに有効とされています。ただし勾配二乗和を蓄積していくため、長く訓練すると学習率が極端に小さくなりすぎる問題があります。
- RMSProp: AdaGradの改良版で、過去の勾配の二乗和を一定の範囲で蓄積（移動平均）することで学習率が極端に下がりすぎないようにした手法です。これも各パラメータに異なる学習率を適応させる点は同じです。RMSPropは主にHintonらによって提唱され、RNNの学習などで威力を発揮しました。
- Adam (Adaptive Moment Estimation): 現在広く使われている最先端の最適化手法の一つです。モーメンタム（勾配の一次モーメント=移動平均）とRMSProp的手法（勾配の二乗の移動平均）を組み合わせており、それぞれをバランスよく考慮することで各パラメータごとに適切なスケールで素早く収束できる更新を行います。要するにMomentum + AdaGrad/RMSPropのハイブリッドで、パラメータごとの学習率調整とモーメンタム加速の両方の利点を持っています。Adamは初期値の設定にもあまり敏感でなく、自動的に学習率調整してくれるため、ディープラーニングにおいてデフォルトで使われることも多いです。
他にもNesterov加速勾配 (NAG)やAdamの改良版（AdamWやAMSGradなど）、最近ではLionやAdaBoundなど様々な最適化手法が研究されています。しかしG検定対策としては、「最適化アルゴリズムは何をするものか」（勾配を使って重みを更新し損失を下げる）と代表的な手法の名前・特徴（SGD, モーメンタム, AdaGrad, Adamなど）をしっかり理解しておけば十分でしょう。例えば「Adamは何を組み合わせた手法か？」や「モーメンタムの効果は？」といった問題が出ても対応できるよう、上記ポイントを整理しておいてください。
G検定で押さえるべきポイント:
- オプティマイザーの役割: 損失関数を最小化するために重みをどう更新するか決めるアルゴリズムである。勾配降下法に基づき、パラメータをどの方向・大きさで動かすかを定める。
- SGDとミニバッチ: 確率的勾配降下法 (SGD)は毎回一つのデータで更新する手法。効率的だが不安定なので、現在はミニバッチ（小さなデータ束）で勾配計算するのが一般的。これにより並列計算もしやすく安定性と速度のバランスが良い。
- モーメンタム: 勾配の移動平均（慣性）を考慮して更新することで、振動を抑え収束を速める。局所最適から抜け出しやすくなる効果もある。
- Adam: 最も重要な高性能オプティマイザーの一つ。モーメンタムによる加速＋勾配二乗平均による学習率調整を組み合わせ、各パラメータを自動調整しながら高速に最適化する。初学者向けには「SGDをより賢くしたもの」という理解でも良いが、名称の由来（Adaptive Moment Estimation）から勾配の1次・2次モーメントを利用していることは知っておこう。
おわりに
以上、ディープラーニングの概要から主要トピック（ニューラルネットワークの構造、活性化関数、誤差関数、正則化、誤差逆伝播法、最適化手法）までを駆け足で解説しました。盛りだくさんでしたが、「層の深いニューラルネットワークを効率よく学習させるための工夫」が各所にあることがお分かりいただけたでしょうか。特にG検定を受験予定の方は、本記事で扱った基本用語や概念は頻出ポイントですので、しっかり整理しておきましょう。
ディープラーニングは奥が深く、本記事で触れた内容も入口にすぎません。しかし基礎概念の習得こそが応用への近道です。ぜひ引き続き公式ガイドブックや信頼できる文献で知識を深めてください。最後までお読みいただき、ありがとうございました！一緒にディープラーニングの学びを進めていきましょう。
G検定対策⑧：AI倫理・AIガバナンスの主要原則と重要用語をわかりやすく解説
AI倫理・AIガバナンスとは？ AI倫理とは、人工知能の開発・利用において守るべき価値観や原則のことです。例えば「AIは人権を尊重すべき」「差別や偏りを生じさせないようにすべき」といった倫理的指針を指します。AIが社会に与える影響が大きくなる中で、何が「良いAI利用」で何が「悪い利用」かを判断する基準として、このAI倫理が重要になります。 一方でAIガバナンスとは、AI倫理を実践するための仕組みやルール作りのことです。企業や政府がAIの開発・運用に際し、適切な管理・監督体制を整え、AIを安全かつ倫理的に活 ...
【G検定対策⑦】AIに関する法律と契約をやさしく解説！個人情報保護法からサービス契約まで
はじめに：AIの法律と契約を学ぶ意義 こんにちは！今回はG検定（ジェネラリスト検定）の合格を目指す皆さんに向けて、AIに関する主要な法律と契約のポイントを講義風にフレンドリーな文体で解説します。AI分野では技術だけでなく法的な知識も求められます。例えば、個人データの扱い方やAIで作った成果物の権利関係を知らないと、思わぬトラブルにつながるかもしれません。法律や契約と聞くと難しく感じるかもしれませんが、数学・法律初心者の方でも理解できるようにやさしく説明していきます。一緒に個人情報保護法からAIサービス提供 ...
G検定初心者向け⑥：AIに必要な数理・統計知識の基礎をやさしく解説
G検定（ジェネラリスト検定）は、AIの基礎知識を問う試験ですが、数学が苦手な方にとってはハードルが高く感じられるかもしれません。ご安心ください。本記事ではAIに必要な数理・統計の知識を、数学初心者でも理解できるように解説します。確率分布の基礎からベイズの定理、分散と標準偏差、そして正規分布まで、G検定で押さえておきたい重要トピックを取り上げます。具体例や図表も交えますので、イメージしながら学んでいきましょう。それでは一緒に基礎を固めていきましょう！ 確率分布とは？離散分布と連続分布の違い まずは確率分布の ...
G検定対策講座⑤：AI社会実装プロジェクトの進め方とデータ分析プロセス徹底解説
はじめに: AIの社会実装とG検定 AI技術を実際のビジネスや社会に役立てる「AIの社会実装」では、技術面だけでなくプロジェクトの進め方やデータの扱い方が重要です。本記事では、講義風かつフレンドリーな口調で、AIプロジェクトの計画から実装までの流れと、データ収集・前処理・分析・学習のプロセスについて解説します。短時間でAI導入のポイントを掴みたいビジネスパーソンは参考にしてください。 1. AIプロジェクトの進め方 AIプロジェクトを成功させるには、明確な目的設定から始まり、段階的にリスクを管理しつつ価値 ...
G検定対策に最適！④ディープラーニング基礎講座：ニューラルネットの概要から誤差逆伝播法・最適化手法まで
はじめに：ディープラーニングの概要 皆さん、ディープラーニング（深層学習）という言葉はもう聞いたことがありますよね？これは人工知能（AI）の一分野で、多層のニューラルネットワークを用いてコンピュータが自らデータから特徴を学習する技術です。従来の機械学習では、どの特徴に注目すべきか人間が設計していましたが、ディープラーニングでは層が深く重なったニューラルネットワークがデータから重要な特徴を自動抽出し、複雑なパターンも捉えられる点が画期的です。2010年代以降、計算資源（GPU）の発達とビッグデータの蓄積によ ...