G検定（ジェネラリスト検定）は、AIの基礎知識を問う試験ですが、数学が苦手な方にとってはハードルが高く感じられるかもしれません。ご安心ください。本記事ではAIに必要な数理・統計の知識を、数学初心者でも理解できるように解説します。確率分布の基礎からベイズの定理、分散と標準偏差、そして正規分布まで、G検定で押さえておきたい重要トピックを取り上げます。具体例や図表も交えますので、イメージしながら学んでいきましょう。それでは一緒に基礎を固めていきましょう！
確率分布とは？離散分布と連続分布の違い
まずは確率分布の概念です。確率分布とは、ある確率変数（結果が不確定な数値）の取り得る値とその確率の対応関係を表したものです。平たく言えば「どのような結果がどれくらいの確率で起こるか」をまとめた分布表のようなものです。例えばサイコロを1回振ったときの出目は1から6までの整数ですが、それぞれの出る確率は約16.7%（1/6）になります。このように、確率変数（結果の値）が取り得る値ごとに確率が定まっている状況を確率分布と言います。
確率分布には大きく分けて離散型と連続型の2種類があります。違いは確率変数の値が「飛び飛びの個別値か（離散）、連続的な値か（連続）」です。離散型確率分布では、確率変数がとる値は0や1、2、3...のように個々の数値として数えられます。一方、連続型確率分布では、値は身長や時間のように連続的な範囲を取り得ます。下表に離散分布と連続分布の特徴をまとめます。
| 分布の種類 | 特徴 | 例（代表的な分布） |
|---|---|---|
| 離散型確率分布 | 確率変数がとる値が個別の値（整数など、数えられる値）になる分布。各値に確率が割り当てられ、その確率の合計は1になる。グラフでは棒グラフ（ヒストグラム）で表せる。 | サイコロの目の分布、ベルヌーイ分布（0/1の二値）、二項分布（例：コイン投げの表の回数）、ポアソン分布（一定時間内の発生回数）など |
| 連続型確率分布 | 確率変数がとる値が連続的（実数の範囲）になる分布。個々の値の確率は厳密には0になるため、確率密度で表現し、ある区間に入る確率として考える（密度曲線の下の面積が1になる）。滑らかな曲線や数式（確率密度関数）で表す。 | 身長・体重や気温の分布、一様分布（0～1の間が均等な分布）、正規分布（後述のガウス分布）など |
離散分布の典型例としてサイコロの出目があります。上の表にも示した通り、1から6のそれぞれに確率1/6が割り当てられる離散型分布です。棒グラフにすると6本の棒がすべて同じ高さ（1/6）になります。一方、連続分布の例として人間の身長を考えてみましょう。身長は連続的な値を取り得るため、「ちょうど170.00cm」のようなピンポイントの値の確率はほぼ0です。その代わり「170cmから171cmの間に収まる確率」といった範囲での確率を考えます。その分布は滑らかな曲線（例えば後述する正規分布に近い形）で表現できます。
G検定で押さえるべきポイント: 確率分布の基本概念と離散型・連続型の違いを理解しましょう。離散分布では確率質量関数（PMF）で各値に確率を割り当て、連続分布では確率密度関数（PDF）で区間ごとの確率を扱うこと、そして代表的な分布名（二項分布・正規分布など）を押さえておくことが重要です。
ベイズの定理と条件付き確率
次にベイズの定理について学びましょう。ベイズの定理は条件付き確率を用いて「ある事象Aが起こったときに別の事象Bが起こる確率」を求めるための公式です。一見難しそうですが、要は「原因と結果の確率をひっくり返す」ための道具だと考えると分かりやすいです。まず条件付き確率とは、何らかの条件の下での確率のことです（例：「雨の日に限って渋滞する確率」など）。ベイズの定理はその条件付き確率同士の関係式として以下のように表されます。
上式は「事象Bが起きたときに事象Aが起きている確率」を表しています。右辺はそれを別の確率で表現したもので、
は「Aが起きたときBも起きる確率」、
は「Aが起きる事前確率（何の情報もない状態でのAの起こりやすさ）」、
は「Bが起きる全体での確率（事前に見たBの起こりやすさ）」です。つまり「結果Bが与えられたときの原因Aの確率」を、「原因Aから結果Bになる確率」と事前の頻度から計算しているわけです。
ベイズの定理のイメージ例
難しく感じる場合は具体例で考えてみましょう。たとえば病気の診断を想像してください。ある珍しい病気Aの有病率（事前確率）が1%だとします。検査Bは病気の人を正しく陽性と判定する確率が95%（感度95%）、健康な人を誤って陽性と判定してしまう確率
が5%（偽陽性5%）だったとしましょう。このとき、検査が陽性(B)だった人が本当に病気(A)である確率
はどのくらいになるでしょうか？
直感的には「陽性だから95%くらいの確率で病気では？」と思うかもしれません。しかしベイズの定理で計算すると以下のようになります。
（1%）
（病気なら陽性になる確率）
全体で陽性となる確率 
（約5.9%）
これらをベイズの式に当てはめると、
つまり約16%となります。意外に低いですよね！この例では病気がまれなので、検査が陽性でも実際に病気である可能性は16%程度しかないのです。ベイズの定理はこのように、直感とは異なる確率を正しく導くために不可欠な考え方なのです。
実際のAI分野でもベイズの定理は重要です。例えばスパムメール判定では、「メールに特定の単語が含まれる(結果B)とき、そのメールがスパムである(原因A)確率」をベイズ推定で計算するナイーブベイズ分類が使われます。また機械学習のモデルでは事前確率と新しいデータから逐次的に確率を更新する際にベイズの考え方が活用されています。
G検定で押さえるべきポイント: ベイズの定理の公式を暗記するだけでなく、各項の意味を理解しましょう。事前確率・事後確率・尤度（条件付き確率）といった用語を押さえ、「結果から原因の確率を求める考え方」であることを説明できるようにします。例えば「はBという条件下でのAの確率」という読み方や、ベイズの定理が機械学習の推論（例：ナイーブベイズ）に応用されている点も理解しておくと万全です。
分散と標準偏差とは？データのばらつきを示す指標
次は統計でよく出てくる分散と標準偏差です。これはデータのばらつき（散らばり具合）を表す指標です。平均値がデータの中心傾向を示すのに対し、分散・標準偏差はデータが平均からどれくらい広がっているかを定量的に示します。G検定では直接計算問題は少ないかもしれませんが、概念として押さえておくことが大切です。
分散とは、一言で言えば「データの平均からのズレを二乗して平均したもの」です。計算式で表すと、データの集合 
の平均を 
としたとき分散
は
と表せます。各データの値と平均との差
を二乗し、その平均をとった値が分散です。「二乗平均」と覚えておくとイメージしやすいでしょう。なぜ二乗するかというと、単純に差を足し合わせると正負が打ち消しあって0になってしまうため、ばらつきを表すには差を二乗して正の値にする必要があるからです。
しかし分散は値を二乗しているため、元のデータの単位とは異なる次元の値になっています。そこで分散の正の平方根を取ったものが標準偏差です。標準偏差
（シグマ記号で表すことが多いです）は、分散の平方根: 
で定義されます。こうすることで元のデータと同じ単位でばらつきを表現できます。例えば身長データの分散が(cm)
の単位で○○であれば、その平方根である標準偏差はcmの単位になり、直感的にも「平均からどのくらい離れているか」を把握しやすくなります。
具体例で考えてみましょう。二つのクラスAとBで数学テストを行い、それぞれの平均点は両方とも70点だったとします。しかしクラスAはどの学生もだいたい65～75点に集中していたのに対し、クラスBは50点台から90点台まで点数がばらばらでした。この場合、平均点は同じ70点でもクラスBの方が成績のばらつきが大きいことになります。数値で示せばクラスBの分散・標準偏差の方がクラスAより大きくなるのです。このように、標準偏差が小さいほどデータは平均付近に集まっており、標準偏差が大きいほどデータの散らばりが大きいと言えます。
G検定で押さえるべきポイント: 分散と標準偏差はセットで理解しましょう。「標準偏差は分散の平方根」という関係（
）を覚えること、そしてデータのばらつき具合を示す指標であることが重要です。名称から何を意味するか（例えば「偏差」とは平均との差のことである）を説明できるようにします。また「平均や中央値が同じでも標準偏差が異なれば分布の広がり方が違う」ことにも注意しましょう。これらはデータ分析や機械学習でデータのばらつきを評価する際に基本となる知識です。
正規分布（ガウス分布）とは？その特徴と重要性
最後に正規分布について解説します。正規分布は統計学で最も重要と言ってよい分布で、別名ガウス分布（ドイツの数学者ガウスにちなむ）とも呼ばれます。正規分布は左右対称の釣鐘型（ベルカーブ）の形状をした連続型確率分布で、平均値を中心にデータが集まり、遠く離れるほど出現確率が低くなるという特徴があります。身長や体重、誤差の分布など、自然界や社会で見られるさまざまな連続値のデータが近似的に正規分布に従うことが知られています。「この世でもっとも一般的な分布」と言われることもあるほどです。
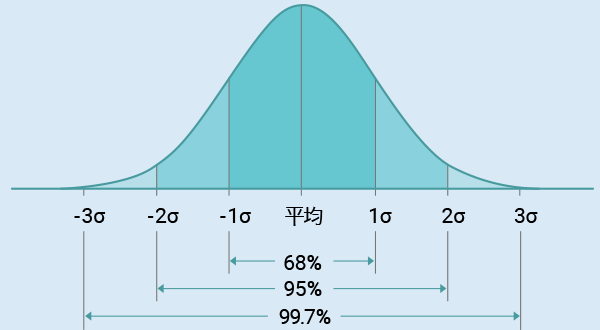
正規分布の典型的な形はこの図のように平均値を中心とした左右対称の釣鐘型です。横軸は確率変数の値、縦軸はそのときの確率密度を表しています。正規分布では平均値＝中央値＝最頻値となり、分布の中心がデータの山の頂点になります。曲線は中心付近が高く両端に向かって滑らかに低くなっていき、x軸に対して漸近的（無限に近づくが接しない）に近づいていきます。標準偏差が大きいほど曲線は横に広がり平坦になり、が小さい（データのばらつきが小さい）ほど尖った形になります。
正規分布には便利な性質がいくつもあります。特に有名なのが「68–95–99.7%ルール」です。これは平均値を中心にした区間にデータがどのくらい入るかを示した経験則で、平均±1標準偏差の範囲に約68%、±2標準偏差で約95%、±3標準偏差でほぼ99.7%のデータが収まるというものです。例えば平均170cm・標準偏差5cmの身長の正規分布なら、約68%の人は165～175cmの範囲に、95%近くは160～180cmの範囲に収まるイメージです。正規分布では標準偏差がこのように具体的な割合に対応するため、データのばらつきを直感的に把握しやすいという利点があります。
また正規分布は統計学・機械学習で前提として扱われることが多い分布です。理由の一つに中心極限定理があります。これは「たくさんの独立した要因の和（平均）は正規分布に近づく」という定理で、誤差や測定値などが正規分布に従いやすい根拠となっています。そのため多くの統計手法が「データは正規分布に従う」という仮定の下で成り立っています（例えば回帰分析の残差の仮定など）。機械学習でもデータの分布を正規分布と仮定してモデルを構築する場合や、正規分布に従う乱数を使って初期重みを設定するニューラルネットワークの手法などがあります。
なお、平均と分散
で指定される正規分布は
と表記します。特に
の標準偏差1の正規分布は標準正規分布と呼ばれ、
と書かれます。この標準正規分布は統計表や計算ソフトで累積確率がよく使われますが、G検定ではそこまで細かい計算は求められないでしょう。重要なのは正規分布の形状と性質を理解していることです。
G検定で押さえるべきポイント: 正規分布は「平均を中心とした釣鐘型の連続分布」であり、統計学で基本となる分布であることを押さえましょう。名称からガウス分布とも呼ばれる点、平均＝中央値＝最頻値となる対称な形状、そして「±1σで68%」などの具体的な特性を覚えておくと試験でも役立ちます。また、「データが正規分布に従う」という仮定がいろいろな手法の基盤になっていることや、中央極限定理によって正規分布が現れる背景にも触れておくと理解が深まります。G検定でも正規分布は頻出用語ですので、そのイメージをしっかり頭に入れておきましょう。
まとめ：G検定に向けて数理・統計の基礎固めをしよう
今回は、G検定対策として数学初心者に向けてAIに必要な数理・統計知識の基礎を解説しました。確率分布の考え方（離散型と連続型の違い）、ベイズの定理による確率の更新、データのばらつきを示す分散と標準偏差、そして重要な正規分布の性質について、それぞれポイントを押さえられたでしょうか。
数学に苦手意識がある方でも、概念のイメージさえ掴めればG検定で問われる基礎知識は怖くありません。実際、G検定は公式や計算そのものよりも概念理解が重視されます。それぞれの用語や定理が「何を意味し、何に使われるのか」をしっかり説明できるようにしましょう。例えば、「ベイズの定理は原因と結果の確率を結びつける考え方」「標準偏差が大きいとデータのばらつきが大きい」といった具合です。
数理・統計分野はディープラーニングやAI理解の土台でもあります。今回整理した内容以外にも、G検定では線形代数（行列やベクトル）、微分・積分、相関や仮説検定などが出題範囲に含まれます。まずは本記事の内容を繰り返し復習し、基礎用語を自分の言葉で説明できるようにしてください。その上で余力があれば他の数学分野も学んでおくと、より安心して試験に臨めるでしょう。
最後に、難しいと感じる部分は身近な例に置き換えて考えてみることをおすすめします。今回紹介したサイコロや身長の例のように、実生活のイメージと結びつけると理解が深まります。継続的な学習で少しずつ自信をつけ、ぜひG検定合格を勝ち取ってください！数学初心者からAIの世界への一歩を応援しています。一緒に頑張りましょう。
G検定対策⑧：AI倫理・AIガバナンスの主要原則と重要用語をわかりやすく解説
AI倫理・AIガバナンスとは？ AI倫理とは、人工知能の開発・利用において守るべき価値観や原則のことです。例えば「AIは人権を尊重すべき」「差別や偏りを生じさせないようにすべき」といった倫理的指針を指します。AIが社会に与える影響が大きくなる中で、何が「良いAI利用」で何が「悪い利用」かを判断する基準として、このAI倫理が重要になります。 一方でAIガバナンスとは、AI倫理を実践するための仕組みやルール作りのことです。企業や政府がAIの開発・運用に際し、適切な管理・監督体制を整え、AIを安全かつ倫理的に活 ...
【G検定対策⑦】AIに関する法律と契約をやさしく解説！個人情報保護法からサービス契約まで
はじめに：AIの法律と契約を学ぶ意義 こんにちは！今回はG検定（ジェネラリスト検定）の合格を目指す皆さんに向けて、AIに関する主要な法律と契約のポイントを講義風にフレンドリーな文体で解説します。AI分野では技術だけでなく法的な知識も求められます。例えば、個人データの扱い方やAIで作った成果物の権利関係を知らないと、思わぬトラブルにつながるかもしれません。法律や契約と聞くと難しく感じるかもしれませんが、数学・法律初心者の方でも理解できるようにやさしく説明していきます。一緒に個人情報保護法からAIサービス提供 ...
G検定初心者向け⑥：AIに必要な数理・統計知識の基礎をやさしく解説
G検定（ジェネラリスト検定）は、AIの基礎知識を問う試験ですが、数学が苦手な方にとってはハードルが高く感じられるかもしれません。ご安心ください。本記事ではAIに必要な数理・統計の知識を、数学初心者でも理解できるように解説します。確率分布の基礎からベイズの定理、分散と標準偏差、そして正規分布まで、G検定で押さえておきたい重要トピックを取り上げます。具体例や図表も交えますので、イメージしながら学んでいきましょう。それでは一緒に基礎を固めていきましょう！ 確率分布とは？離散分布と連続分布の違い まずは確率分布の ...
G検定対策講座⑤：AI社会実装プロジェクトの進め方とデータ分析プロセス徹底解説
はじめに: AIの社会実装とG検定 AI技術を実際のビジネスや社会に役立てる「AIの社会実装」では、技術面だけでなくプロジェクトの進め方やデータの扱い方が重要です。本記事では、講義風かつフレンドリーな口調で、AIプロジェクトの計画から実装までの流れと、データ収集・前処理・分析・学習のプロセスについて解説します。短時間でAI導入のポイントを掴みたいビジネスパーソンは参考にしてください。 1. AIプロジェクトの進め方 AIプロジェクトを成功させるには、明確な目的設定から始まり、段階的にリスクを管理しつつ価値 ...
G検定対策に最適！④ディープラーニング基礎講座：ニューラルネットの概要から誤差逆伝播法・最適化手法まで
はじめに：ディープラーニングの概要 皆さん、ディープラーニング（深層学習）という言葉はもう聞いたことがありますよね？これは人工知能（AI）の一分野で、多層のニューラルネットワークを用いてコンピュータが自らデータから特徴を学習する技術です。従来の機械学習では、どの特徴に注目すべきか人間が設計していましたが、ディープラーニングでは層が深く重なったニューラルネットワークがデータから重要な特徴を自動抽出し、複雑なパターンも捉えられる点が画期的です。2010年代以降、計算資源（GPU）の発達とビッグデータの蓄積によ ...